Новости – Сергей Губенко, 24.04.2020: Развитие эпидемии коронавируса COVID-19 в Москве. Прогноз.
Эпидемии коронавируса. Аналитические расчёты и прогнозы
Оглавление
Введение
Математические модели
Расчёты по модели SEIR для Москвы
Расчёты по модели SEIRD для России, Германии и США.
Аналитический метод расчёта эпидемии
Эпидемия в Германии
Эпидемия в Китае
Эпидемия в Италии
Эпидемия в Бельгии
Заключение
Литература
Введение
Эпидемии коронавируса COVID-19 охватили большинство стран на планете и 11-го марта 2020 года ВОЗ объявила о пандемии. Сейчас все страны находятся на различных стадиях эпидемического процесса: в одних эпидемия только начинается или находится в самом разгаре; в других – подошли к пику заболеваний или недавно его преодолели; в третьих странах уже победили это заболевание или близки к победе. В борьбе с этим вирусом в мире были предприняты различные меры – от жесткого карантина до полного бездействия. Страны несут огромные экономические потери. Вирус выявил реальное состояние систем здравоохранения и их мобилизационные возможности, а также выявил способности руководителей принимать правильные и своевременные решения. При каких условиях могут приниматься правильные меры по организации карантинных мер и, в дальнейшем, мер по выходу из карантина? Необходимое условие – руководство должно быть ответственным, здравомыслящим, решительным и иметь экономические возможности. Но этого мало, недостаточно. Руководство должно иметь достоверную информацию и опираться на мнение квалифицированных специалистов в этой области, которые обладают научными знаниями, умеют разрабатывать и применять различные достоверные количественные модели и, на их основании, делать ответственные прогнозы и рекомендации. Это должен быть звёздный час этих учёных, к их мнению сейчас прислушиваются президенты, премьеры, губернаторы и мэры. Есть ли у нас в стране такие специалисты? Хотелось бы надеяться, что есть, либо остались старые советские, либо молодые появились. Если ещё не успели реформировать под корень все старые советские системы – образования, здравоохранения и науки, вместе с Академией Наук. Хотя некоторые тревожные заявления меня беспокоят. Приведу несколько из них.
„Нам нужен хороший профессиональный прогноз, на период 3, 7, 10 дней“ (В.В. Путин, 13 апреля 2020 г).
„Ни одна математическая модель, которая сегодня существует, в РФ не подтвердилась“ (Т.А. Голикова, 13 апреля).
„Обеспечить формирование краткосрочного прогноза количества граждан, которые могут заболеть новой коронавирусной инфекцией“ (В.В. Путин, 18 апреля).
Из этих заявлений следует, что на 13 апреля высшее руководство страны не обладало профессиональным прогнозом даже на 3-10 дней и к 18 апреля такой прогноз не появился. Странно. Ведь сделать такой краткосрочный прогноз, относительно, не сложно. Напомню, что эпидемия в России началась 5-го марта (1 человек) и к 13-му апреля (18 328 человек) уже были фактические данные о росте числа инфицированных аж за 40 дней! Это уже много точек и, даже без всякой теории, по ним можно подобрать функцию (степенную, показательную или другую) и проэкстраполировать её вперёд на 3-7 дней. Вот и будет достаточно точный, и почти научный, краткосрочный прогноз. Но, судя по заявлению Президента от 18 апреля, и такой прогноз у него не появился.
На основании чего же тогда наше высшее начальство принимало и принимает ответственные решения по борьбе с эпидемией? Это мне не известно. Однако, сейчас, в конце мая, мне уже ясно, что эти решения и по стране, и по Москве были, в основном, верными и, в основном, своевременными.
Математические модели
Кратко рассмотрим существующие математические модели, описывающие эпидемический процесс. Первая успешная попытка описания распространения болезни была, по-видимому, сделана Даниилом Бернулли в 18-м веке. После него многие математики занимались этими проблемами. Например, в 1840 – м году У. Фарр применил нормальное распределение к анализу смертности от оспы.
Модель SIR. Большинство современных моделей опираются на модель SIR, которую разработали в 1927 году британские учёные А. Кермак и У. Маккендрик. В этой модели популяция разбивается на три группы: число восприимчивых – S, число инфицированных – I, число выздоровевших – R. В группу «восприимчивые» попадают ещё не инфицированные и не имеющие иммунитет. Все эти три функции зависят от времени. Взаимодействие между этими группами описывает система из трёх, не сложных, дифференциальных уравнений, правда, содержащих нелинейность (произведение двух функций). Система не имеет аналитического решения, но легко решается численными методами. Система имеет всего два эмпирических (подгоночных) параметра. Один параметр (β) отвечает за интенсивность инфицирования при контактах, а второй (γ) отвечает за интенсивность выздоровления инфицированных. Отношение β/γ обозначается R0 и называется базовый коэффициент воспроизведения. Если R0 меньше единицы, то очевидно, что эпидемия сама затухает. В литературе сообщают, что эта модель хорошо описывает эпидемии гриппа в больших городах.
Модели SIRS и SIS учитывают, что после некоторых эпидемий люди, после того как переболеют, могут иметь временный иммунитет или не иметь иммунитет вообще.
Модель SEIR учитывает наличие инкубационного периода.
В случае опасной эпидемии это может затруднить своевременное обнаружение массового заражения. Эта модель содержит уже четыре дифференциальных уравнения и имеет четыре параметра. И базовый коэффициент воспроизведения уже определяется этими четырьмя параметрами. Для тех читателей, которые заинтересуются более подробным описанием этих моделей могу порекомендовать статью Павла Бузина «Эпидемии. Модели» (nplus1.ru – "Зараза, гостья наша. Как математика помогает бороться с эпидемиями" [1] (26.12.2019)).
Расчёты по модели SEIR для Москвы
Модель SEIR — одна из самых распространённых. Моделирование позволяет определить: 1) скорость распространения эпидемии, 2) число заразившихся, 3) число больных в критическом состоянии, 4) число умерших. Кроме того, эта модель позволяет оценить эффективность различных мер для подавления эпидемии.
В 2020 году эта модель была доработана швейцарскими учёными – были учтены особенности эпидемии коронавируса. Расчеты по этому новому варианту SEIR сделал Михаил Тамм и интернет-издание «Медуза» опубликовало 30 марта этого года результаты исследования с прогнозами развития эпидемии в Москве (meduza.io – "В Москве ввели жесткие карантинные меры. Похоже, это правильно: математическая модель показывает, что иначе могли бы погибнуть больше 100 тысяч человек — Meduza" [2] (30.03.2020)). Приведём, близко к тексту оригинала, некоторые выводы из этого исследования:
1. "В столице России необходимо — и как можно раньше — резкое сокращение контактов между людьми. Только так можно подавить эпидемию, не допустить перегрузки медицинских учреждений и избежать тысяч жертв".
2. "В случае если бы власти Москвы и России не предприняли никаких мер сдерживания, к сентябрю в столице от коронавируса умерли бы 117 тысяч человек. Пик эпидемии пришелся бы на середину мая, после чего она затухла бы сама (из-за того, что большая часть населения переболела и приобрела иммунитет). На пике потребовалось бы 48 тысяч реанимационных коек (в реальности в городе в марте было 2,5 тысячи коек)".
3. "Слабые меры сдерживания эпидемии, вроде тех, что были введены властями до 28 марта, снизили бы количество умерших за время эпидемии до 92 тысяч человек, а количество критических больных составит 32 тысячи на пике эпидемии (он случится позже, чем в варианте без сдерживания, — в начале июня), так что медицинская система не сможет оказать помощь всем нуждающимся. И это при условии, что второй волны эпидемии не произошло бы".
4. "Радикально изменить ситуацию могли только жесткие меры подавления эпидемии, включающие запрет на выход на улицы без необходимости и наказания за нарушение карантина. Это сделано на этой неделе, поэтому от коронавируса умрет всего 250 человек, а в реанимации на пике (в середине апреля) единомоментно окажется не более 80 больных. Если бы жесткий карантин ввели позже, то количество умерших и потребность в койках реанимации выросли бы на порядок".
Что можно сказать об этом прогнозе? Хорошо, что М. Тамм обратил внимание властей на серьёзность ситуации и на необходимость введения срочных мер, ограничивающих контакты. Однако этот прогноз сильно преувеличил позитивные результаты принятых мер. Неизвестно, знали московские власти этот прогноз или нет, но хорошо, что они, в срочном порядке, начали готовить новые места в больницах, иначе была бы катастрофа.
Расчёты по модели SEIRD для России, Германии и США.
Таких расчётов, наверняка, сделано много, но мы, кратко, рассмотрим всего одну работу молодого российского математика А. Каримова «Пандемия глазами математика, или почему классическая модель SEIRD не работает» (habr.com – "Пандемия COVID-19 глазами математика, или почему классическая модель SEIRD не работает / Хабр" [3] (04.05.2020,)). Автор совершенно справедливо отмечает, что модель SEIR не годится для описания эпидемии COVID-19 хотя бы потому, что в этой модели скрытые носители инфекции Е незаразны и для учёта их заразности вводится ещё один параметр. Итого имеем четыре обыкновенных дифференциальных уравнения первого порядка, содержащие пять параметров. Система решалась численным методом. Значения параметров задавали из соображений здравого смысла, а начальные данные для S, E и I выбрали из данных для России на 2 апреля. Расчёты провели на период со 2-го до 24 апреля. Согласие расчётных и фактических данных оказалось неудовлетворительным, поэтому была проведена оптимизация (подгонка) параметров. После такой подгонки данные стали прекрасно согласовываться, однако новые значения параметров оказались совершенно не приемлемыми, с точки зрения их начального смысла. Для того, чтобы выйти из этой ситуации, автор предложил ввести в систему уравнений ещё одну функцию времени с ещё двумя параметрами и подобрать их так, чтобы урезонить предыдущие пять параметров. Это получилось. Автором был сделан прогноз негативного сценария для России на конец июня – более 300 тысяч зарегистрированных заболеваний и более 10 тысяч смертей.
Таким образом математическое моделирование эпидемических процессов, в настоящий момент, заключается в составлении систем из 3-5 обыкновенных дифференциальных уравнений и решении этих систем численными методами. Эти модели содержат 5-7 подгоночных параметров и, насколько мне известно, не имеют аналитических решений.
Аналитический метод расчёта эпидемии
Не умаляя значения и важности математического моделирования и не заменяя его, хочу предложить относительно простой приближенный аналитический (инженерный) метод расчёта эпидемического процесса.
Метод основан на аппроксимации зависимостей числа инфицированных (выздоровевших, умерших) известными функциями, содержащими 3-4 параметра. Если процесс роста числа инфицированных уже идёт, то эти параметра вычисляются из фактических уже имеющихся данных, например за первый месяц. Важно только правильно выбрать такие функции и как можно точнее определить параметры.
Рассмотрим метод подробнее, и, для начала, введём обозначения.
Пусть
|
Ninf | – общее число инфицированных на данный момент людей;
| |
Ns | – число болеющих на данный момент людей (дома и в больницах);
| |
Nr | – число выздоровевших людей;
| |
Nd | – число умерших.
|
Все эти четыре функции времени (t) связаны очевидным уравнением:
|
Ninf = Ns + Nr + Nd |
. (1) |
Рассмотрим, вначале качественно, какой вид имеют эти функции.
Три функции – Ninf, Nr и Nd - должны иметь похожую форму. До начала эпидемии эти функции равны нулю; затем идёт медленный рост; затем ускорение роста до максимума; затем уменьшение скорости роста постепенно до нуля и, наконец, выход функций на насыщение к концу эпидемии. Таким образом эти монотонно возрастающие функции должны либо точно быть равны нулю до начала и после эпидемии, либо они должны иметь две горизонтальные асимптоты (N=0 и N=Nmax) и точку перегиба, в которой первая производная имеет максимум, а вторая производная равна нулю.
В процессе эпидемии, помимо абсолютных значений Ninf, Nr и Nd ,
фиксируются также их ежедневные (ежесуточные) приросты ΔNinf,
ΔNr и ΔNd. Эти функции до начала эпидемии и после её окончания равны нулю и где-то внутри этого промежутка имеют максимумы.
Опустим временно индексы и проведём общие рассуждения для N и ΔN. Заметим, что дифференциал функции равен
dN = N’t × dt .
Эпидемия продолжается примерно 100 дней, поэтому в качестве дифференциала переменной можно взять Δt=1 день и получим приближённо ΔN = N’t . Просуммировав (проинтегрировав) все ΔN получим N. Исходя из этих простых соображений для N и ΔN и можно подбирать вид функций F(t) и f(t), причём F’(t) = f(t). Отметим, что такие простейшие пары функций, как t2 и 2t; sin(t) и cos(t); eat и a×eat и тому подобные – не подходят, так как не удовлетворяют перечисленным выше условиям (асимптоты у F(t) и максимум у f(t)). Хотя фактические данные показывают, что на начальном этапе функции ведут себя как растущие экспоненты, ясно, что для всего периода эпидемии функции должны иметь более сложный вид.
Таких функций достаточно много, но мы рассмотрим всего две.
Напомним из теории вероятностей два распределения, а именно – нормальное и логнормальное, и приведём их формулы и графики.
Нормальное распределение. Случайная величина X распределена по нормальному закону, если она имеет плотность вероятности (дифференциальную функцию) и, соответственно, интегральную функцию следующего вида:
|
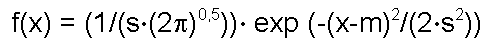
|
, (2) |
|
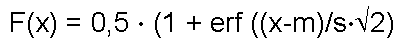
|
, (3) |
где m и s – параметры нормального распределения, и в этом распределении m – это, одновременно, математическое ожидание, среднее, мода и медиана; а s – среднеквадратическое отклонение, а дисперсия равна s2.
Графики этих функций приведены на рис 1.
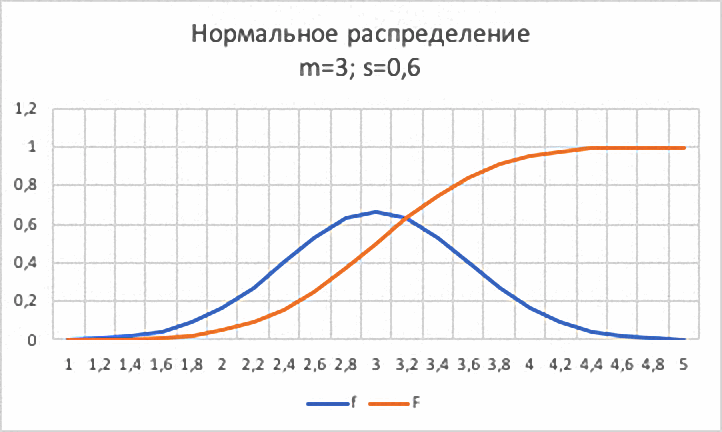
Рис.1. Плотность вероятности f(x) и интегральная функция F(x).
Нормальное распределение.
Видим, что f(x) имеет колоколообразную симметричную форму, а функция F(x) имеет так называемую S- образную форму и имеет две горизонтальные асимптоты F(x)=0 и F(x) = 1. Параметр m – среднее значение принят равным 3. Изменяя этот параметр можно перемещать всю картинку вдоль оси x.
Логнормальное распределение. Логарифм случайной величины распределён по нормальному закону. Плотность распределения и интегральная функция имеют вид:
|
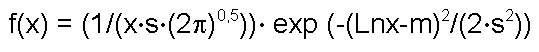
|
, (4) |
|
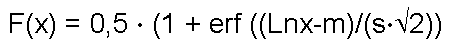
|
, (5) |
где m и s – просто параметры логнормального распределения, а для вычисления среднего значения, моды, дисперсии и других характеристик существуют простые формулы, которые мы не будем здесь приводить.
Графики этих функций приведены на рис 2.
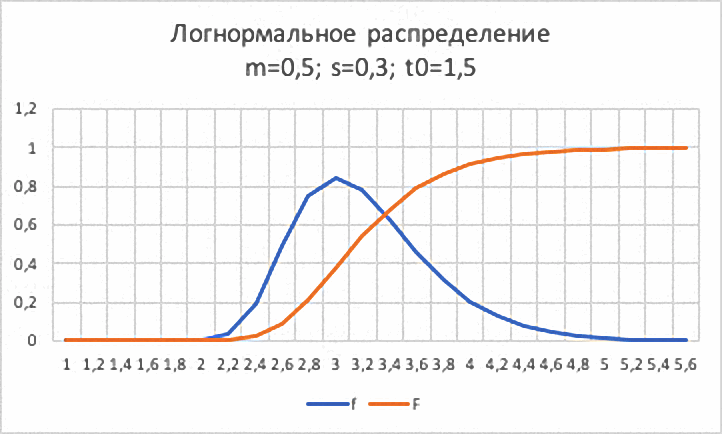
Рис.2. Плотность вероятности f(x) и интегральная функция F(x).
Логнормальное распределение.
В этом распределении x>0. Видим, что f(x) тоже имеет колоколообразную, но не симметричную форму. Асимметрия – правосторонняя. Функция F(x) имеет S- образную форму и имеет горизонтальную асимптоту F(x) = 1 при x®¥. F(x) и f(x) ®0 при x®0. Параметр m, в данном распределении, не отвечает за перемещение всей картинки вдоль оси x. Для того чтобы появилась такая возможность, пришлось ввести ещё один параметр x0, и заменить в формулах x на (x-x0).
Поэтому на рис. 2 для того, чтобы переместить картинку от начала координат вправо, в район x=3, подобрали значение x0=1,5.
Теперь пришло время поблагодарить теорию вероятности за предоставленные формулы, временно забыть про вероятностный смысл этих формул и, слегка изменив их, попробовать применить их к эпидемическому процессу. Изменения: 1) заменим переменную x на время t, 2) домножим правую сторону уравнений на постоянный множитель N0, имеющий смысл – конечного числа инфицированных (умерших, выздоровевших).
Расчётные (логнормальные) формулы принимают вид:
|
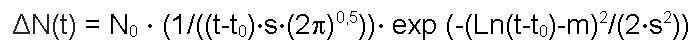
|
, (6) |
|
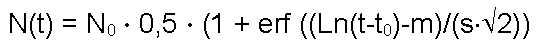
|
. (7) |
В интегральных функциях присутствует специальная функция erf (z), которая носит название Интеграл вероятности или Функция ошибок.
Вычислять erf (z) можно либо с помощью таблиц; либо используя онлайн калькулятор; либо, что совсем просто, используя последние версии Excel.
Возникает вопрос, какие формулы использовать “нормальные” или “логнормальные”? Оказалось, что на начальных этапах кривые инфицирования хорошо описываются и теми и другими формулами. Если имеем уже достаточно фактических данных (например, более 50), то выбор можно сделать по виду зависимости ΔN(t), если она асимметрична, то – вторые. Для тех стран, для которых проведены расчёты в этой статье, выбраны именно вторые (логнормальные) формулы.
Параметры (N0 ; m ; s ; t0 ) необходимо подобрать так, чтобы расчётная кривая как можно лучше описывала фактические (экспериментальные) значения. Это задача оптимизации. Составляем целевую функцию и находим её минимум, варьируя параметры. Это можно сделать либо вручную и “на глазок”, наблюдая как расчётная кривая сближается с реальной, при изменении значений параметров, либо можно использовать специальную программу. В качестве целевой функции можно выбрать среднеквадратичное отклонение расчётных значений от фактических на каком-то массиве данных.
Таким образом получаем расчётные уравнения для числа инфицированных (Ninf), числа выздоровевших (Nr) и числа умерших (Nd).
Расчётное уравнение для числа болеющих получаем из уравнения (1), то есть Ns = Ninf - Nr - Nd.
Какие цели будем преследовать при проведении этих расчётов?
1. Выясним, насколько хорошо эти формулы описывают эпидемические процессы (инфицирование, выздоровление или смерть) на большом промежутке времени, например, 3 месяца. То есть число точек должно быть порядка 90.
2. Выясним, насколько хорошо эти формулы позволяют делать прогноз, хотя бы на 10-15 дней.
Приведём примеры таких расчётов для некоторых стран.
Эпидемия в Германии
Первые инфицированные появились в Германии в конце февраля 2020 года. Так 25 февраля их было 18; 1-го марта 130; 5-го марта 545; 8-го марта 1040; 15-го марта уже 5813 и далее эпидемия начала набирать обороты. Для получения уравнений были выбраны фактические статистические данные числа инфицированных Ninf, числа выздоровевших Nr и числа умерших Nd в первых 77 дней эпидемии (с 1-го марта и по 16 мая).
Результаты вычислений параметров (N0 ; m ; s ; t0 ) и среднеквадратического отклонения SN точек расчётной кривой от фактических данных представлены ниже.
|
N = (N0 ; m ; s ; t0 ) и SN |
, |
|
Ninf = (185000 ; 3,55 ; 0,45 ; 0 ) SN = 242 |
, |
|
Nr = (176000 ; 3,8 ; 0,42 ; 5,2 ) SN = 169 |
, |
|
Nd = (8710 ; 3,72 ; 0,39 ; 6,97 ) SN = 7 |
. |
Несколько слов об этих значениях параметров. Напомню, параметры N0 имеют смысл конечных величин числа инфицированных, выздоровевших и умерших за всё время эпидемии. Они правдоподобны. То, что процесс инфицирования начинается в начале, а выздоровления и смерти начинаются через несколько дней, это тоже понятно, поэтому и появляется не нулевое значение параметра t0 . Теперь об отклонениях SN . Если учесть, что основная масса данных имеет значения тысяч и десятков тысяч, то такие отклонения следует признать маленькими, а, следовательно, совпадение расчётных и фактических данных признать хорошим.
Это видно и на рис 3, на котором рассчитанные по формулам (7) значения (линии) и фактические значения (точки), практически, совпадают.
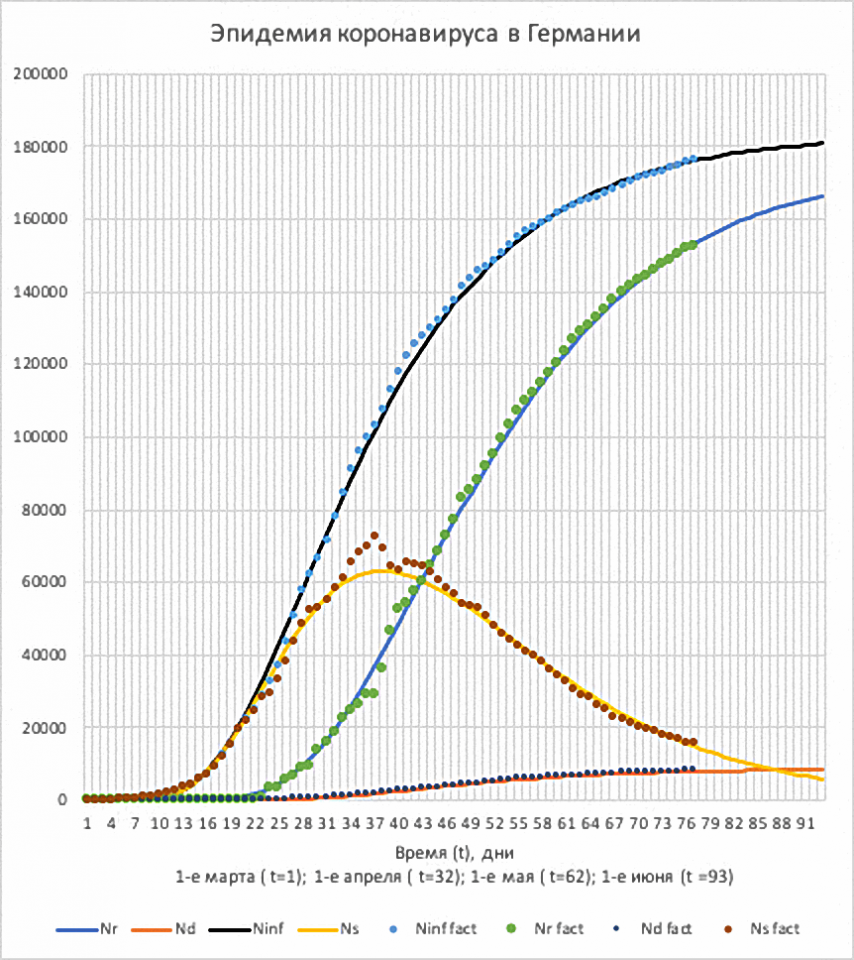
Рис.3. Эпидемия в Германии. Изменение со временем
числа инфицированных (Ninf); числа выздоровевших (Nr);
числа умерших (Nd) и числа болеющих (Ns).
Расчёты – линии, фактические данные – точки.
Напомним, что параметры одни и те же у соответствующих пар функций – N(t) и ΔN(t).
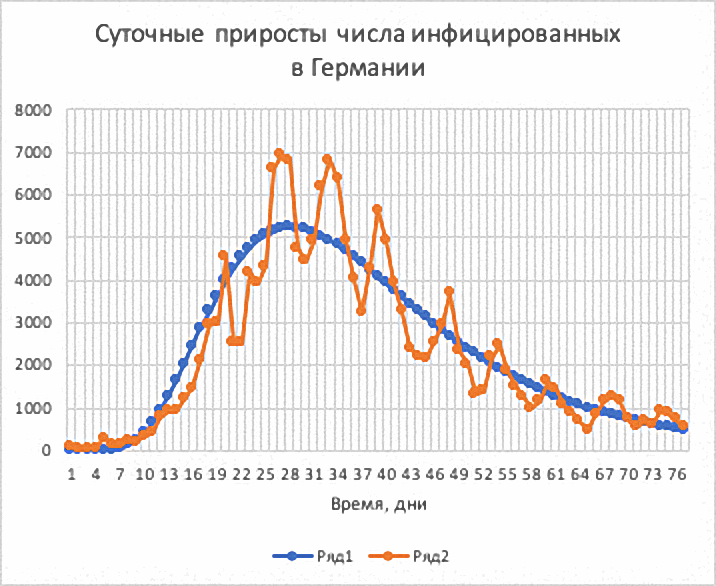
Рис.4. Суточные приросты числа инфицированных ΔNinf.
Синие точки – расчётные значения, оранжевые – фактические.
Виден разброс фактических значений относительно расчётной кривой. Этот разброс таков, что, при желании, в районе максимума можно увидеть и “плато”. Из этих данных также видно, что зависимость имеет явно выраженную правостороннюю асимметрию.
Таким образом – на протяжении 77 дней от начала эпидемии, предложенные формулы хорошо описывают процессы.
Теперь проверим, насколько хорошо эти формулы могут прогнозировать ситуацию. Напомним, что оптимизация параметров была проведена на результатах до 16-го мая, поэтому спрогнозируем по этим формулам ситуацию на 30-е мая, то есть через 14 дней. Результаты представлены в таблице.
|
Прогноз на 30.05.2020 |
Фактически 30.05.2020 |
Ошибка |
|
Ninf |
180 221 |
183 189 |
1,6 % |
|
ΔNinf |
216 |
267 |
19,1% |
|
Nr |
164 791 |
164 908 |
0,1% |
|
Nd |
8 370 |
8 530 |
1,9% |
Видим, что совпадение по числу инфицированных, числу выздоровевших и числу умерших очень хорошее и ошибка не превышает 2%. Ошибка по приростам больше и составляет 19%, но это тоже объяснимо, так как наблюдается большой разброс этих данных (см. рис. 4).
Таким образом, можно считать точным прогноз на 14 дней.
Эпидемия в Китае
Китай был первой страной, где началась эта эпидемия и он первый с ней успешно справился. Официальные данные приводятся с 23 января 2020 года, в этот день было уже 830 инфицированных. Далее 24.01 – 1287; 25.01 – 1975; 26.01 – 2740; 27.01 – 4515 и далее рост ускорился. Из этих данных видно, что эпидемия началась не 24-го января, а 5-8 дней раньше, где и должно было быть время начала отсчёта эпидемии.
Для расчётов выбрали первые 85 точек (с 23 января и по 16 апреля) и провели оптимизацию параметров. В результате получили:
|
N = (N0 ; m ; s ; t0 ) SN и SDN |
, |
|
Ninf = (83000 ; 3,1 ; 0,36 ; – 5 ) SN = 240, SDN =132 |
, |
|
Nr = (77200 ; 3,59 ; 0,34 ; 0 ) SN = 123, SDN =31 |
, |
|
Nd = (3350 ; 3,15 ; 0,54 ; 0 ) SN = 34, SDN =14 |
. |
Видно, что для Ninf получили отрицательный параметр t0 = -5, но это и понятно, так как эпидемия началась не 23-го, а несколькими днями раньше. Все отклонения не велики, поэтому согласие расчётных и фактических данных хорошее.
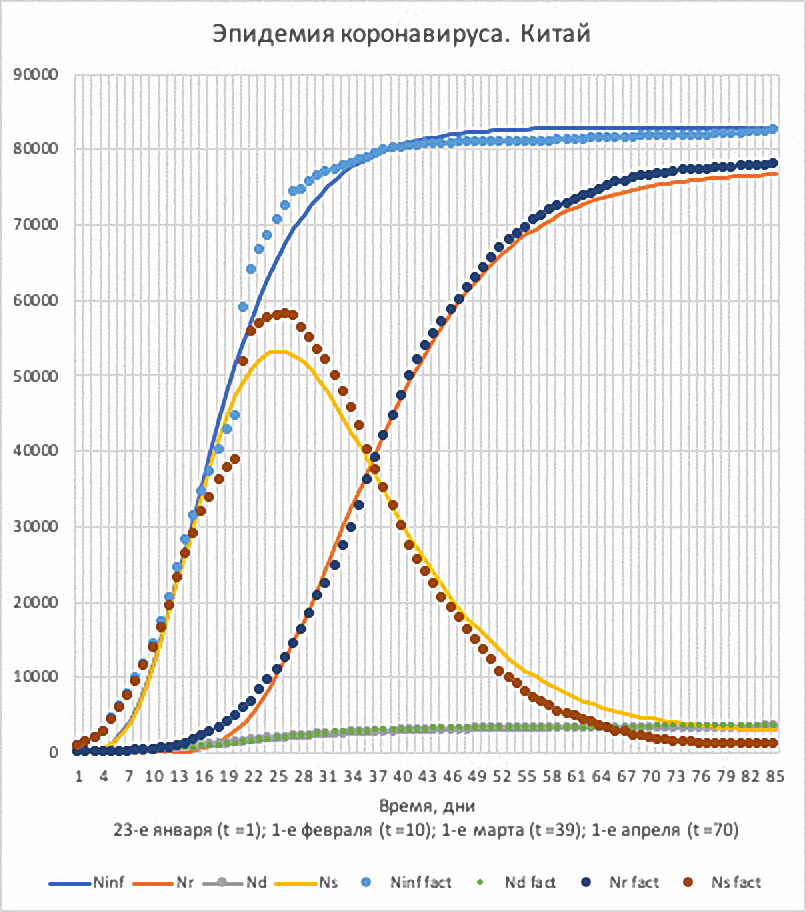
Рис.5. Эпидемия в Китае. Изменение со временем
числа инфицированных (Ninf); числа выздоровевших (Nr);
числа умерших (Nd) и числа болеющих (Ns).
Расчёты – линии, фактические данные – точки.
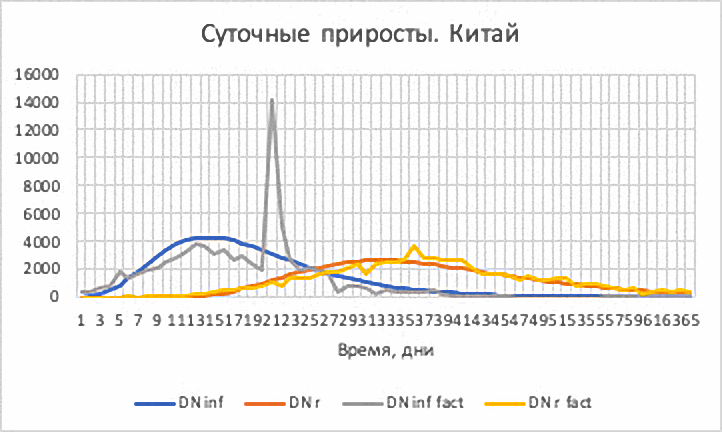
Рис.6. Китай. Суточные приросты:
— числа инфицированных DN inf (расчёт) и DN inf fact
— числа выздоровевших DN r (расчёт) и DN r fact.
t=1 (23.01.2020); t=10 (01.02.2020); t=39 (01.03.2020); t=70 (01.04.2020)
На рис. 5 и 6 представлены кривые эпидемического процесса и суточные приросты. Обращает на себя внимание, что 12-го февраля (t=21) был большой одноразовый скачок приростов числа инфицированных. Скачок составил 14,1 тыс. хотя до этого несколько дней приросты были по 2-3 тысячи. Причины этого мне не известны. Такой большой скачок приростов, естественно, привёл и к слому фактической зависимости числа инфицированных (рис. 5).
Прогнозы делать не будем, так как эпидемия закончилась.
Эпидемия в Италии
В Италии эпидемия началась в середине февраля. Согласно статистике, число инфицированных: 16.02 – 3 человека; 20.02 – 4; 21.02 – 21; 22.02 – 79; 23.02 – 157; 26.03 – 470; 29.02 – 1128 и быстрый рост далее.
Для расчётов выбрали первые 92 точки (с 16-го февраля до 17-го мая) и провели оптимизацию параметров. В результате получили:
|
N = (N0 ; m ; s ; t0 ) SN |
, |
|
Ninf = (235 300 ; 3,86 ; 0,405 ; 0 ) SN = 176 |
, |
|
Nr = (210 000 ; 4,32 ; 0,46 ; 10 ) SN = 325 |
, |
|
Nd = (35 500 ; 3,8 ; 0,49 ; 8,5 ) SN = 18 |
. |
Отклонения небольшие, согласие фактических и расчётных данных хорошее.
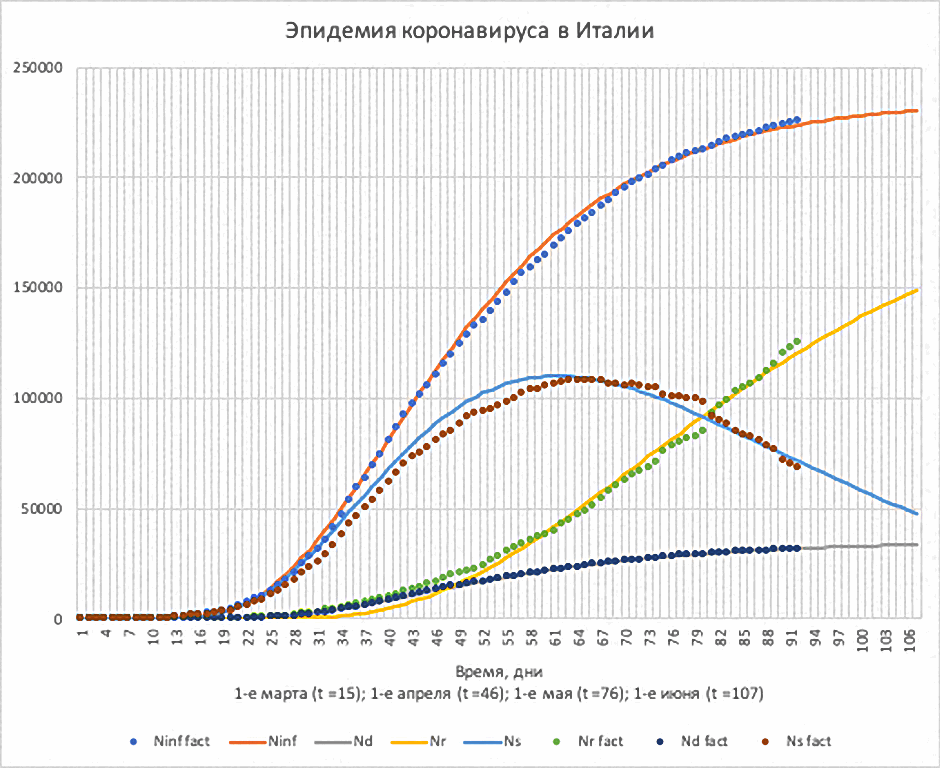
Рис.7. Эпидемия в Италии. Изменение со временем
числа инфицированных (Ninf); числа выздоровевших (Nr);
числа умерших (Nd) и числа болеющих (Ns).
Расчёт – линии, фактические данные – точки.
Видно, что кривая инфицирования уже вышла на насыщение, а кривая выздоровевших ещё нет, поэтому пока достаточно большое число больных, порядка 50 000 человек (синяя кривая).
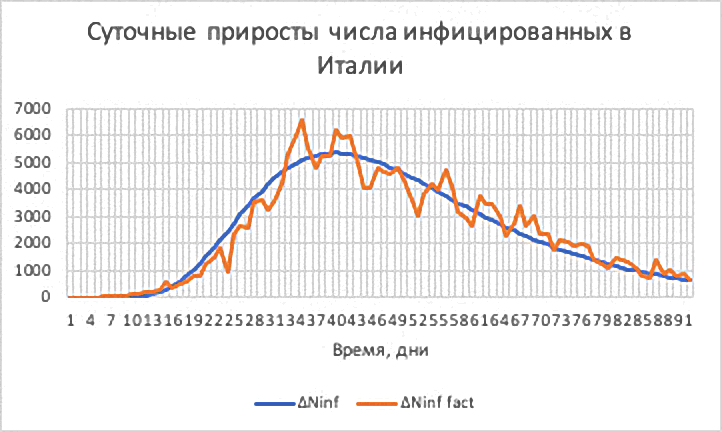
Рис.8. Италия. Суточные приросты числа инфицированных
DN inf (расчёт) и DN inf fact (фактически).
На рис 8 представлены приросты числа инфицированных. Чётко выраженная правоассиметричная кривая. Кстати, на фактической кривой явно прослеживается некая периодичность с периодом несколько дней. Похожая картинка была и в Германии (рис. 4).
Теперь спрогнозируем ситуацию на 30-е мая, то есть на 13 дней вперёд после 17-го мая (последней точки оптимизации параметров). Результаты представлены в таблице.
|
Прогноз на 30.05.2020 |
Фактически 30.05.2020 |
Ошибка |
|
Ninf |
229 755 |
232 664 |
1,3% |
|
ΔNinf |
308 |
414 |
26,0% |
|
Nr |
147 495 |
155 633 |
5,2% |
|
Nd |
33 521 |
33 340 |
— 0,5% |
Эти результаты прогнозирования также можно признать хорошими.
Эпидемия в Бельгии
В Бельгии статистика ведётся с 16 февраля, но был всего 1 инфицированный человек, вплоть до 29 февраля. Реальный рост инфицированных начался в марте: 01.03 – 2; 03.03 – 15; 04.03 – 23; 06.03 – 109; 13.03 – 559; 16.03 – 1058 и рост усилился. Рост числа выздоровевших начался с 17 марта (было 14 человек), а рост числа смертей начался с 16 марта (было 10 случаев).
Для расчётов, выбрали первые 95 точек (с 16-го февраля до 20-го мая) и провели оптимизацию параметров. В результате получили:
|
N = (N0 ; m ; s ; t0 ) SN и SDN |
, |
|
Ninf = (60 000 ; 3,77 ; 0,4 ; 14 ) SN = 51 , SDN = 25 |
, |
|
Nr = (16 000 ; 3,65 ; 0,48 ; 23 ) SN = 15 , SDN = 9 |
, |
|
Nd = (9 500 ; 3,7 ; 0,35 ; 21 ) SN = 53 , SDN =18 |
. |
Отклонения не большие, согласие фактических и расчётных данных хорошее.
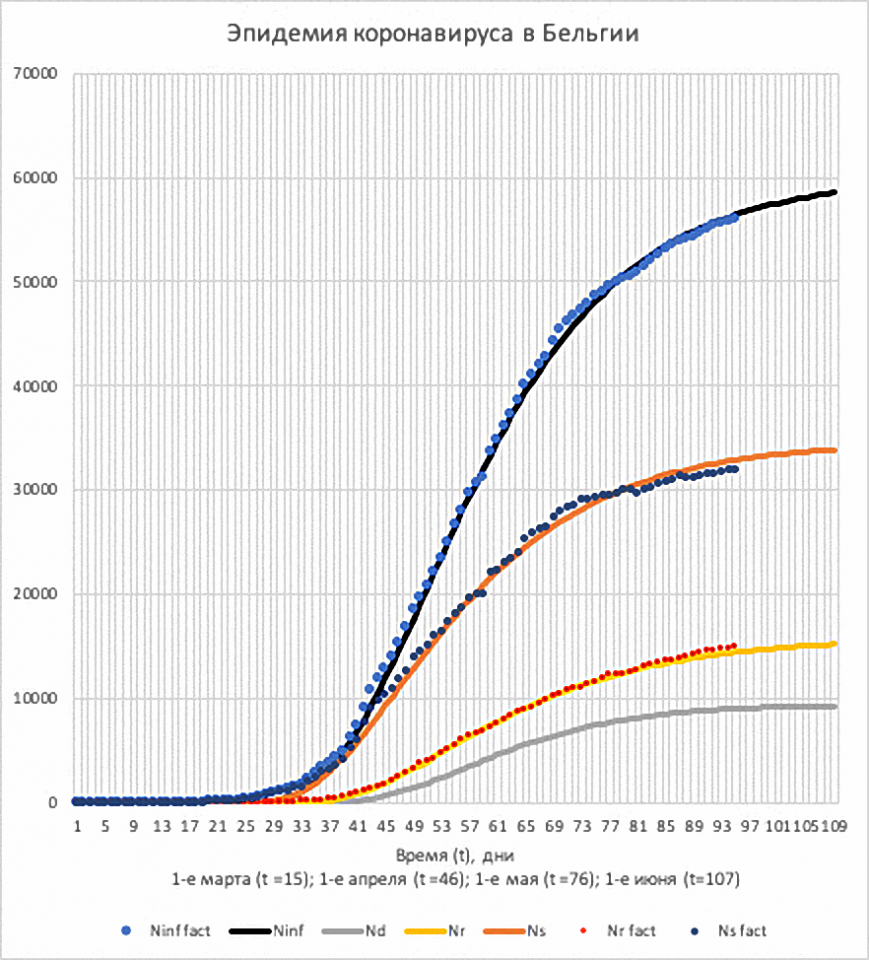
Рис.9. Эпидемия в Бельгии. Изменение со временем
числа инфицированных (Ninf); числа выздоровевших (Nr);
числа умерших (Nd) и числа болеющих (Ns).
Расчёты – линии, а фактические значения – точки.
Согласие хорошее. Видно, что кривая инфицирования уже выходит на насыщение, а кривая выздоровевших ещё нет, поэтому пока достаточно большое число больных (более 30 000 человек).
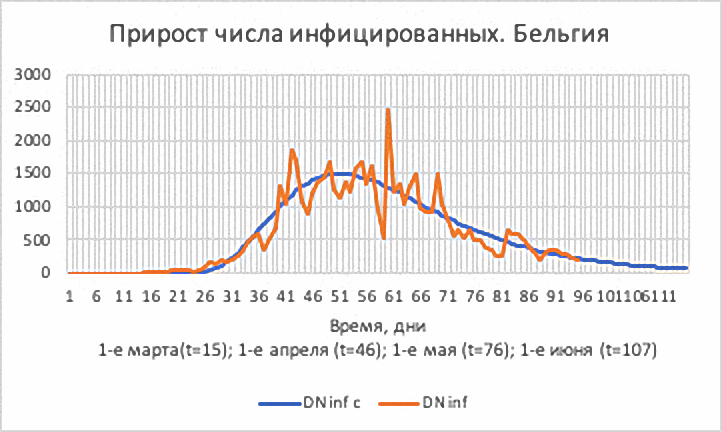
Рис.10. Бельгия. Суточные приросты числа инфицированных
DN inf c (расчёт) и DN inf (фактические данные).
Видно, что кривая приростов асимметрична. Разброс большой.
Плато пройдено.
Сделаем прогноз для Бельгии на 10 дней вперед (на 30-е мая). Результаты в таблице.
|
Прогноз на 30.05.2020 |
Фактически 30.05.2020 |
Ошибка |
|
Ninf |
58 080 |
58 186 |
0,2% |
|
ΔNinf |
118 |
125 |
5,6% |
|
Nr |
15 081 |
15 769 |
4,4% |
|
Nd |
9 299 |
9 453 |
1,6% |
Согласие очень хорошее для всех величин.
Заключение
Математическое моделирование распространения эпидемий находится в России не на должном уровне. Эту ситуацию необходимо срочно исправлять. Без научного прогнозирования трудно принимать своевременные и адекватные меры.
В данной статье автор предлагает относительно простой аналитический метод расчёта процесса распространения эпидемии. Метод основан на аппроксимации уже полученных данных соответствующими функциями и оптимизации параметров этих функций. Вид этих функций взят из теории вероятности (нормальное и логнормальное распределение), но в функции введено время, как переменная.
Данный метод ни в коей мере не заменяет математическое моделирование.
На основании предложенного метода, в качестве примеров, проведены расчёты эпидемических процессов в Германии, Китае, Италии и Бельгии. Предложенные формулы позволяют описывать процессы в течение длительного периода (порядка трёх месяцев) а также делать прогнозы. Согласие расчётных данных и прогнозов с реальными данными хорошее.
В дальнейшем планируется провести подобные расчёты для других стран и, в первую очередь, для России.
Литература
[1] – | П. Бузин. Эпидемии. Модели
Зараза, гостья наша. Как математика помогает бороться с эпидемиями
26.12.2019
nplus1.ru/material/2019/12/26/epidemic-math
"Современные математические модели позволяют очень хорошо учитывать важнейшие параметры, влияющие на распространение и интенсивность эпидемий — плотность популяции, наличие инкубационного периода у заболевания, частоту контактов, карантины, вакцинацию и другие. Результаты моделирования хорошо согласуются с экспериментальными данными. Все вместе это дает человечеству надежду на то, что пандемии прежних масштабов нам больше не грозят".
|
[2] – | М.Тамм. Коронавирусная инфекция в Москве: прогнозы и сценарии.
В Москве ввели жесткие карантинные меры. Похоже, это правильно: математическая модель показывает, что иначе могли бы погибнуть больше 100 тысяч человек — Meduza
30.03.2020
meduza.io
"Скорее всего, многим читателям может показаться, что автор их специально пугает: вывод о возможности 110–120 тысяч смертей от коронавируса в Москве звучит одновременно и жутко, и неправдоподобно".
Использованная для расчетов модель построена Рихардом Нейером (Университет Базеля) с сотрудниками и доступна по адресу https://covid19-scenarios.org
|
[3] – | А. Каримов. Пандемия COVID-19 глазами математика, или почему классическая модель SEIRD не работает.
04.05.2020, 15:20
habr.com/ru/post/500348/
"Я нарочно привел в статье только негативный сценарий, когда мы повторяем судьбу США в плане динамики эпидемии. Если этот сценарий окажется верным, к концу июня у нас будет более 300 тыс. зарегистрированных случаев заболевания и более 10 тысяч смертей. Хотя есть предпосылки к тому, что этот сценарий не воплотится в реальности, я бы посоветовал отнестись к нему по принципу: «надейся на лучшее, готовься к худшему». Как говорится, если уж за борьбу с эпидемией в США взялись лучшие умы НАСА, значит, дело и правда скверное".
|
Сергей Губенко
|